Getting started - a minimal autoencoder¶
I like the idea of autoencoders - part of the difficulty of working with GCM output is that there is so much of it, an automatic system for reducing it to a more manageable size is very appealing. So I looked for a very simple TensorFlow autoencoder example, and chose the first one from Vikram Tiwari’s tf.keras Autoencoder page.
- To follow that example, but using 20CR2c MSLP fields instead of MNIST as the target, I made three changes:
- I used the 20CR2c data source.
- I changed the activation from
relutotanhas the normalised mslp data is spread around 0 rather than on the range 0-1. - I changed the loss metric to RMS from
binary_crossentropy(because this is a regression problem, not a classification).
#!/usr/bin/env python
# Very simple autoencoder for 20CR prmsl fields.
# Single, fully-connected layer as encoder+decoder, 32 neurons.
# Very unlikely to work well at all, but this isn't about good
# results, it's about getting started.
import os
import tensorflow as tf
#tf.enable_eager_execution()
from tensorflow.data import Dataset
from glob import glob
import numpy
import pickle
# How many times will we train on each training data point
n_epochs=100
# File names for the serialised tensors to train on
input_file_dir=("%s/Machine-Learning-experiments/datasets/20CR2c/prmsl/training/" %
os.getenv('SCRATCH'))
training_files=glob("%s/*.tfd" % input_file_dir)
n_steps=len(training_files)
train_tfd = tf.constant(training_files)
# Create TensorFlow Dataset object from the file names
tr_data = Dataset.from_tensor_slices(train_tfd)
# Use all the data once each epoch
tr_data = tr_data.repeat(n_epochs)
# Present the data in random order
# ?? What does buffer_size do?
tr_data = tr_data.shuffle(buffer_size=10)
# We don't want the file names, we want their contents, so
# add a map to convert from names to contents.
def load_tensor(file_name):
sict=tf.read_file(file_name) # serialised
ict=tf.parse_tensor(sict,numpy.float32)
return ict
tr_data = tr_data.map(load_tensor)
# Also need to reshape the data to linear, and produce a tuple
# (source,target) for model
def to_model(ict):
ict=tf.reshape(ict,[1,91*180])
return(ict,ict)
tr_data = tr_data.map(to_model)
# Make similar dataset for testing
test_file_dir=("%s/Machine-Learning-experiments/datasets/20CR2c/prmsl/test/" %
os.getenv('SCRATCH'))
test_files=glob("%s/*.tfd" % test_file_dir)
test_steps=len(test_files)
test_tfd = tf.constant(test_files)
test_data = Dataset.from_tensor_slices(test_tfd)
test_data = test_data.repeat(n_epochs)
test_data = test_data.shuffle(buffer_size=10)
test_data = test_data.map(load_tensor)
test_data = test_data.map(to_model)
# That's set up the Datasets to use - now specify an autoencoder model
# Input placeholder - treat data as 1d
original = tf.keras.layers.Input(shape=(91*180,))
# Encoding layer 32-neuron fully-connected
encoded = tf.keras.layers.Dense(32, activation='tanh')(original)
# Output layer - same shape as input
decoded = tf.keras.layers.Dense(91*180, activation='tanh')(encoded)
# Model relating original to output
autoencoder = tf.keras.models.Model(original, decoded)
# Choose a loss metric to minimise (RMS)
# and an optimiser to use (adadelta)
autoencoder.compile(optimizer='adadelta', loss='mean_squared_error')
# Train the autoencoder
history=autoencoder.fit(x=tr_data, # Get (source,target) pairs from this Dataset
epochs=n_epochs,
steps_per_epoch=n_steps,
validation_data=test_data,
validation_steps=test_steps,
verbose=2) # One line per epoch
# Save the model
save_file="%s/Machine-Learning-experiments/simple_autoencoder/saved_models/Epoch_%04d" % (
os.getenv('SCRATCH'),n_epochs)
if not os.path.isdir(os.path.dirname(save_file)):
os.makedirs(os.path.dirname(save_file))
tf.keras.models.save_model(autoencoder,save_file)
# Save the training history
history_file="%s/Machine-Learning-experiments/simple_autoencoder/saved_models/history_to_%04d.pkl" % (
os.getenv('SCRATCH'),n_epochs)
pickle.dump(history.history, open(history_file, "wb"))
This runs nicely on my Linux desktop - takes about s/epoch (with 315 training fields) and uses 6 cores (of 8). The validation loss falls from around 0.5 to 0.19 over 100 epochs. So it’s learning something.
To see exactly what it does, we can compare an original MSLP field with the same field passed through the autoencoder (after 100 epochs training):

MSLP contours from 20CR2c for 2009-03-12:12. Original in top panel - after passing through the autoencoder in bottom panel.
The result is not bad, considering the simplicity of the model (32 neurons, only a few minutes training time - it gets the subtropical highs and the storm tracks.
Because the model is so simple, we can also examine the weights directly:
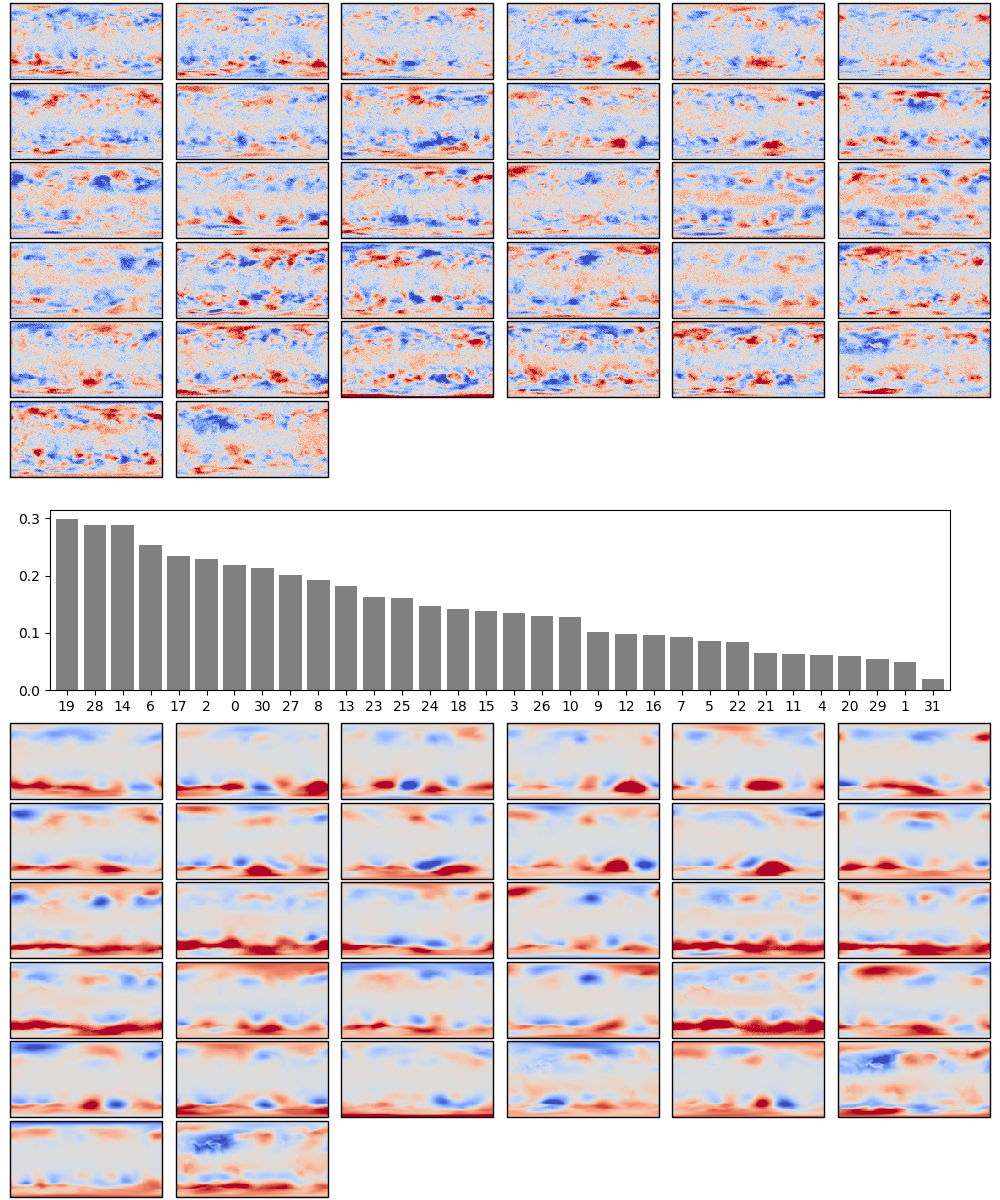
Weights after 100 epochs training. The boxplot in the centre shows the weights associated with each neuron in the hidden layer, arranged in order, largest to smallest. Negative weights have been converted to positive (and the sign of the associated output layer weights switched accordingly). The colourmaps on top are the weights, for each hidden layer neuron, for each input field location (so a lat:lon map). They are aranged in the same order as the hidden layer weights (so if hidden-layer neuron 3 has the largest weight, the input layer weights for neuron 3 are shown at top left). The colourmaps on the botton are the output layer weights, arranged in the same way.
The weights show the model is behaving sensibly, I expected it to converge on a set of output patterns similar to EOFs of the pressure field, a matching set of input patterns, and a range of hidden-layer weights indicating which patterns were typicaly bigger. We do get something that looks like that.
So it does work, though not well enough to be useful. Success is then merely a matter of specifying and training a better model.